In “Using Dynamic Asset Allocation to Boost Returns” I wrote:

The projected P/E ratio can help us decide where to invest. If one index’s projected P/E ratio implies it is relatively cheap and another that it is relatively expensive, overweighting the inexpensive index should boost investment returns.

For example, take the projected P/E for the Russell 2000 small cap divided by the projected P/E ratio for the Russell 1000 large cap. This ratio of P/E ratios averages about 1.033. Small cap has a slightly higher P/E ratio because people are willing to pay a little more for a small-cap stock. Although the mean ratio of P/E ratios is close to 1, the standard deviation is 0.122. One standard deviation is a good measurement to use. When the ratio is as high as 1.155, the market is signaling that small cap is relatively expensive and large cap relatively cheap. An allocation tilted more toward large cap should do better. And when the ratio is as low as 0.911, one standard deviation, the market is signaling that small cap is relatively cheap and should outperform in the coming months. Tilting dynamically between asset categories can boost returns even more than asset allocation.

Here is the chart showing R2000 P/E divided by R1000 P/E (projected) on the X-axis against the difference in next month’s large minus small returns on the Y-axis. As you can see, although the scatter plot is all over the place, the trend is that when large is relatively cheap, large out performs and when small is cheap it outperforms.

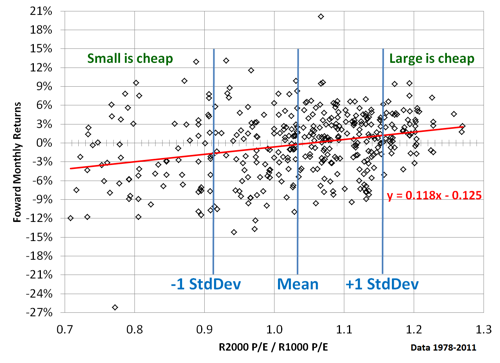
Currently large is relatively cheap and small cap is relatively expensive. For that reason, the R1000 or S&P 500 should outperform the R2000 small cap.

Subscribe to Marotta On Money and receive free access to the presentation: The Ten Best ETFs of 2012.