Over the past few weeks we’ve been examining the investment science behind asset allocation. We learned that risk generally follows return. We learned that tilting small and value can boost returns. And we learned that blending investments near the efficient frontier can make even more efficient portfolios.
In our fall conference at Dimensional Funds, Eugene Fama presented the U.S. market returns from 1927 through 2010. He broke them down into 25 style boxes, each representing two deciles of size and value measurements. Style boxes were made popular by Morningstar as a visual representation of size and valuation. Morningstar divides each axis in thirds, but the data we looked at divided each axis in fifths to make a 5 by 5 grid. Each style box from micro-cap value to mega-cap growth had a computation of its monthly mean return and standard deviation to locate it on the efficient frontier.
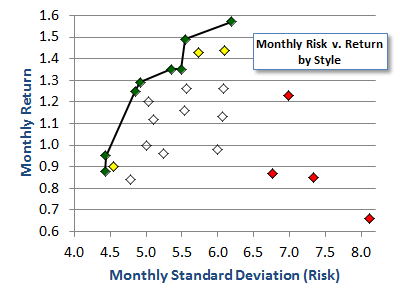
If the capital asset pricing model (CAPM) represented the entire formula for risk and return, each of the 25 points would be along the efficient frontier in a relatively straight line. But this is not the case. Only 8 of the points were so obviously efficient that no other point had a higher return with a lower standard deviation. Three additional points were nearly as efficient so only one other data point was more efficient.
Given a longer time period, the efficiency of each box would possibly become more apparent, but this does not seem to be the case. At least four boxes do not appear to be anywhere next the efficient frontier because they have high volatility and low returns. There also seems to be a pattern of efficiency curving from large-cap blend down through mid-cap value to small-cap value.
As I have explained previously, not everything is on the efficient frontier. In this case, it appears as though small-cap growth has higher volatility and lower returns than every other category. This situation is both as unusual as it is unexplainable.
It does not appear to be an initial public offering (IPO) effect. Most IPOs are trading below their initial valuation two years after the company goes public. Many of them fall into the small-cap growth category. But even after accounting for these, the category still has higher volatility and lower returns.
In the Fama-French three-factor model, the value factor has a greater effect than the size factor. This is because of the poor performance of small growth. Whatever the reason, reducing your allocation to small-cap growth, on average, should boost your returns and lower your volatility.
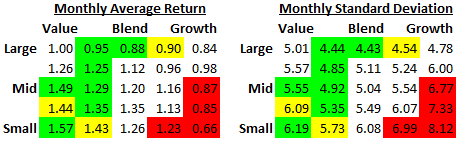
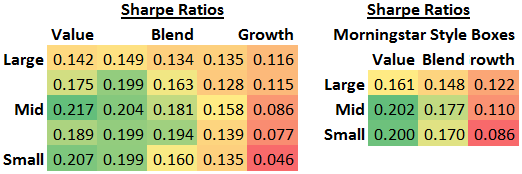
In the investing world the Sharpe ratio, named for Nobel prizewinning economist William Sharpe, measures efficiency. It is the amount of excess return above the risk-free rate divided by the standard deviation. I used the equivalent of 3.5% annually for the risk-free rate and computed Sharpe ratios for each style box. This produced Sharpe ratios ranging from 0.046 through 0.217. I also translated the 5-by-5 grid to the more familiar Morningstar 3-by-3 grid.
Sharpe ratios suggest where you should be investing your money. But they do not specify a corresponding asset allocation. We could use efficient frontier calculations. Over any specific time period, however, that might eliminate entirely decent investments that are just slightly off the efficient frontier.
Picking and choosing to invest in specific asset classes comes with a cost. And one of the important principles of efficient investing is that costs matter. Total stock market indexes come with very low expense ratios. Any investment that picks and chooses from among smaller asset classes has to justify returns exceptional enough to overcome higher expense ratios. A better investment strategy allows investments off the efficient frontier. But it underweights them by some ratio of their distance from the efficient frontier.
I made up my own algorithm for computing an asset allocation from a collection of Sharpe ratios. Much of investing wisdom is simple rules of thumb to help you make relatively smart decisions quickly, easily and accurately. It is not hubris to use such methods to approximate a precise decision in an imprecise world. In fact, that’s the very way we got the Sharpe ratio. Perhaps in the future this methodology will be called the “Marotta allocation method.”
The method involves first squaring the Sharpe ratio of each asset category. A small Sharpe ratio such as the 0.046 of micro-cap growth becomes an even smaller 0.002. The larger 0.217 Sharpe ratio of mid-cap value is not reduced as much and ends up as 0.047.
From the resulting numbers I created an allocation where each category gets a proportional allocation of the 100% total. Where the micro-cap growth starts as 21% of the size of mid-cap value, after squaring the Sharpe ratios, ends up as less than 5%. Squaring makes the small allocations tiny.
So the Marotta allocation method is a proportionally weighted allocation based on the square of each Sharpe ratio. Squaring the Sharpe ratio drastically reduces asset categories in proportion to their distance from the efficient frontier.
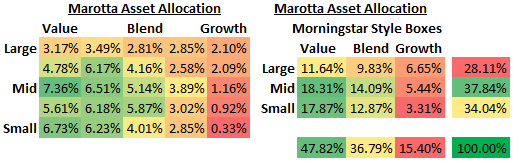
For the traditional Morningstar style boxes, this translates to investing only 3.31% in small-cap growth while allocating 18.31% to mid-cap value. And it means 47.82% on the value side and only 15.40% in growth. It also implies 37.84% in mid-cap and only 28.11% in large cap. These asset allocations may seem to tilt more toward the small and value side than many investors are familiar with. Historically, however, this allocation would produce better risk-adjusted returns.
This allocation is relatively easy to approximate with a simple portfolio of low-cost exchange-traded funds. Invest 20% in Vanguard S&P 500 (VOO), 10% in Vanguard S&P 500 Value Index ETF (VOOV), 30% in Vanguard Mid-Cap Value ETF (VOE), 20% in Vanguard Small Cap Value ETF (VBR) and 20% in iShares Russell 2000 Value Index (IWN). This allocation produces a very efficient portfolio for an expense ratio of only 0.19%.
Although this is an excellent static asset allocation, next week we will learn how to add a dynamic component to boost returns even more.