A group of our advisors attended a conference this past fall sponsored by Dimensional Fund Advisors. In his talk, “Risk Dimensions of the Market,” Eugene F. Fama reviewed the latest data on the Fama-French three-factor model for investment returns.
Modeling investment returns seeks to find an equation to predict your expected returns as much as possible. The simplest equation for the markets would be “Return equals 11.71%.” This has been the average return from 1927 through 2010, the zero factor model. Put your money in the market, and you will get, on average, 11.71% annually.
E(Ri) = E(Rm)
Where:
E(Ri) is the expected return on an investment
E(Rm) is the expected return of the market (about 11.71%)
The one-factor model, called the capital asset pricing model (CAPM), was developed in the early 1960s. William Sharpe, Harry Markowitz and Merton Miller won the Nobel Prize in economics for this work. CAPM adds a single factor to the equation: risk as measured by standard deviation.
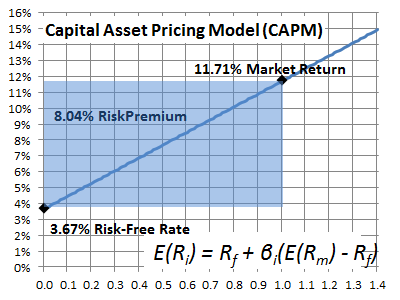
CAPM claims that the riskier the stock, the greater its expected return. Historical analysis provides evidence of how much. The CAPM formula says that the 11.71% returns of the market are actually a risk-free return of 3.67% plus a premium of 8.04% that investors require to take the risks in an inherently volatile stock market.
E(Ri) = Rf + (E(Rm) – Rf)
Where:
Rf is the risk-free rate of interest (about 3.67%)
for example what you could get in short term Treasuries
(E(Rm) – Rf) is sometimes called the market premium (about 8.04%)
the difference between the expected market rate of return and the risk free rate of return.
CAPM goes on to state that although the average premium for investing in the market is 8.04%, the premium is higher on more volatile stocks and lower on less volatile stocks. In other words, investors demand and receive a higher expected return for more volatile stocks. The sensitivity of a stock to market volatility is called “beta.”
The beta of a stock measures the likely movement of a specific investment against the actual movement of the market. If the x-axis is the movement of the market and the y-axis is the movement of a specific investment, a line can be graphed of the average for all the movements of the market and the corresponding movements of a specific investment. The formula for the expected return of an investment is the risk-free return plus the stock’s beta times the risk premium.
E(Ri) = Rf + βi(E(Rm) – Rf)
Where:
βi = Cov(Ri, Rm) / Var(Rm)
the sensitivity of the expected excess asset returns to the expected excess market returns.
For example, a stock with a beta of 2.0 will go up twice the market premium when the stock market goes up. But it will go down twice as much when the market goes down. Because the market generally trends upward, this stock has a higher expected return. A stock with a beta of only 0.5 will be less volatile but also have a lower expected return.
Individual stocks do not follow these trends exactly. They are only aggregate trends. The more heavily diversified you are and the longer you are invested in the markets, the more your experience will coincide with market averages. But the general idea that systematic risk and average return go together is the important lesson for investing.
Three caveats to note. Systematic risk is undiversifiable market risk. Many investment schemes involve specific risks that can and should be avoided. Also, typically the market is measured by the S&P 500, which ignores the fact that this index only represents a portion of the investable markets. Finally, your experience of market returns is diminished by the fees and expenses of your investment vehicles. Hidden costs are often a significant drag on your specific portfolio investments.
There is no such thing as a safe investment that pays market rates of return. Safe investments average 3.67% annually. If you want the other 8.04%, you must be willing to put your money at risk. You can and should be prudent, but there is no guarantee that you will get all your money back. The general principle is that risk follows return.
CAPM is the one-factor model for investment returns. Next week we will add two more factors that help explain more of the variance of specific investments against general market returns. In the meantime, we learn from CAPM that the markets are inherently volatile but also very profitable. Historically, the market has paid a premium for risk. And although we cannot avoid systemic risk, we can steer clear of specific risks and high fees and expenses.
7 Responses
Austin English
What a great concise explanation of risk/return conversation. A great follow up to this article may revolve around inflation. Without including inflation in an individual’s investment strategy, I worry that they may be lulled into false securities thinking a 3+% of risk free return is enough growth to return adequate return for future retirement needs.
Once again, great article!
David John Marotta
Greetings Austin, You are correct, the risk-free rate of return doesn’t even keep up with inflation and provides a much lower standard of living in retirement. I suggest reading my article “Investing Mostly in Bonds Means a Lower Lifestyle in Retirement.”
Greg Vermeychuk
Mr. Marotta,
Thank you for the well-written article on CAPM. I would argue that the so-called ‘riskless rate of return’ does not exist any more. Under ordinary circumstances, the return on any investment can be decomposed into a riskless rate plus a premium. Although the US Treasury cannot ever technically default, since its debts are Dollar denominated and the Govt can create as many dollars as needed, what happens when confidence is eroded to the point where Treasury yields climb above some of the AAA Corporates, such as Microsoft and ADP? Do we consider a corporation ‘riskless’ and impute a sovereign risk premium to Treasury debt? I would like to have your comments on this issue. Thanks in Advance.
David John Marotta
Greetings Greg, GREAT question. The riskless rate of return is a theoretical idea and not bound to the United States. Perhaps it is Swiss Francs, Canadian dollars, Australian dollars or New Zealand dollars. The more the risk or reality of the devaluation of the U.S. dollar the less a Treasury yield reflects the riskless rate of return. As you suggest, in that case Treasury yields would climb above the riskless rate. Nothing guarantees that anyone has to offer a riskless investment. See my article, “Cash Has Been the Riskiest Investment.”
Kevin Brosious
Thanks David, good stuff, looking forward to your next article.
Question about one of your statements: “CAPM adds a single factor to the equation: risk as measured by standard deviation.”
Should this be beta instead of std deviation since std deviation measures total risk (systematic and non-systematic) and beta measures only systematic risk? The only reward is for assuming systematic risk since non-systematic risk can be diversified away.
David John Marotta
Greetings Kevin, You are correct, CAPM adds the factor of beta, which is what multiple of the market volatility is reflected in the stock’s volatility. This is roughly the same as standard deviation, as, on average, a stock with a beta of 1.2 will have a 120% of the volatility of the markets as measured by standard deviation.
Kevin Brosious
Good discussion Dave,
Perhaps on avg the std and beta are close, but there can be a very big difference in some individual stocks/funds.